箱ひげ図の作り方と構成要素の意味

データの分布を説明するために箱ひげ図が用いられます。統計のグラフとしてはとても大切なグラフです。
箱ひげ図(ボックスプロット)とは
箱ひげ図は、「箱」とそこから伸びる「ひげ」を用いて分布の様子を表現するグラフです。データの分布を見る方法として、ヒストグラムや度数分布を用いることもありますが、そこからは大まかな情報は得られるが正確な値を図表から読み取るのは困難です。
そこで、もう少し詳細に分布の形状を明らかにするために分位数(または分位点)が用いられます。分位数とは、データを大きさの順に並べ、データ全体をいくつかのグループに観測値の個数で等分した際の境界となる値で、データ全体を4等分した場合の四分位数はよく用いられます。

それぞれの境界を「第1四分位数」「第2四分位数(中央値)」「第3四分位数」と呼び、これに「最小値」と「最大値」を加えた、5つの数をまとめて5数要約と呼びます。
極端な観測値(外れ値)があると、データ分析において大きく影響を受けるため、外れ値の影響を避けるために中央値に近い半分の観測値を含む長さを散らばりの尺度として考えることが多いです。
この散らばりの尺度として利用されるのが、四分位範囲(第3四分位数−第1四分位数):Inter Quartile Range、IQRと呼び、この尺度は外れ値の影響をほとんど受けません。
参考までに、IQR×1.5からはみ出る値を外れ値として取り扱うことが多いようです。
Tableauでの箱ひげ図の作り方
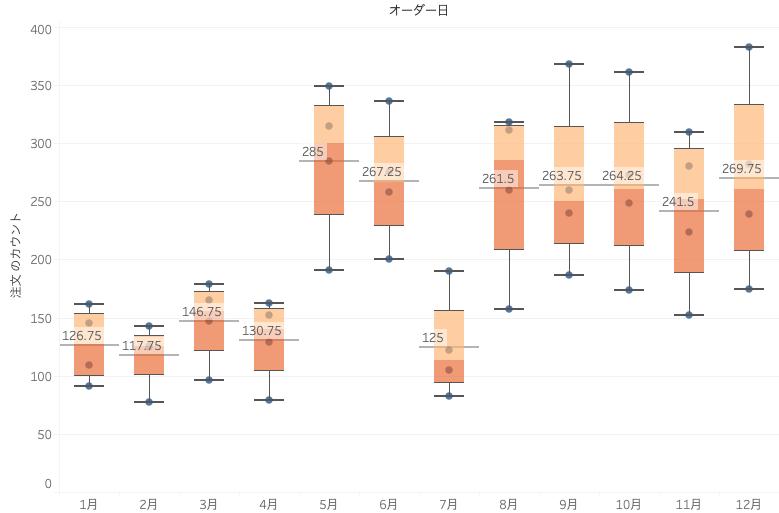
SAMPLE:スーパーストアを用い、ある月における注文数の分布を並列箱ひげ図を用いて表現してみたいと思います。そして、平均値線も引いてみたいと思います。

ここまで読んでいただいてありがとうございます。参考になれば幸いです。
分布を表現するグラフにヒストグラムがあります。以下のページで作り方を紹介していますので、合わせて確認してください。